Programmi

Cliccando sui link che vedi in basso potrai visionare alcuni programmi scritti usando i linguaggi VB.Net o C#. Ovviamente ogni programma presente in uno di questi link avrà un suo “gemello” nell’altro: in questo modo potrai sicuramente capire ancora meglio le differenze e le analogie presenti in questi due linguaggi di programmazione.

VB.Net :https://drive.google.com/drive/u/0/folders/1-_AxRXmhRJyIgw2zITij4qnOY2xNX1sY

C#: https://drive.google.com/drive/u/0/folders/1jXvjU-XkQpWgYc7cVTd5MNbZynsojBVI

Qui in basso troverai la descrizione di ogni programma scritto, con particolare attenzione alle strutture utilizzate per scrivere ognuna di esse:

• Progetto C: in questo progetto sono presenti tutte le funzioni elementari scritte usando il linguaggio C#. La sua progettazione prevede l’utilizzo di 5 bottoni, 3 TextBox ed una Label ed esegue 4 funzioni diverse:
  1. Scrivendo una parola nella TextBox in alto a sinistra e cliccando il bottone affianco apparirà nella Label sottostante (inizialmente vuota) la stessa parola data in input preceduta da “Ciao, “.
  2. Fa riferimento ai due bottoni centrali e alla casella Label utilizzata nella funzione precedente. Cliccando uno di questi due bottoni avrete in output una frase diversa a seconda di quale avete premuto. Per progettare questa funzione ho utilizzato il comando if all’interno di una sola funzione per entrambi i bottoni.
  3. Fa riferimento al bottone e alla TextBox posizionati in basso. Cliccando il bottone verrà visualizzata nella casella di testo l’unione di due stringhe espresse in maniera esplicita all’interno del programma.
  4. L’ultima funzione utilizza gli strumenti posizionati a destra del form. Posizionando il cursore sul bottone, la casella di testo cambierà colore (si avrà lo stesso esito, seppur con colori diversi anche cliccando il bottone o allontanando il cursore da questo). Inoltre, fare click sul bottone restituirà anche una parola presente in maniera esplicita nel programma.
• TipiDiDatiC: in questo progetto sono stati introdotte le principali tipologie di dati (non mi dilungherò sulla descrizione dei dati poiché queste informazioni sono presenti nell’articolo 7 che troverete in questo blog). Sono state create, inoltre, una Reference Type e una Value Type al fine di mostrare le particolarità che le contraddistinguono mediante il programma stesso.
• ArrayMediaC: questo programma necessita l’inserimento di una coppia di numeri pari in input. Una volta inseriti questi numeri verranno creati due array contenenti rispettivamente tutti i numeri pari e dispari compresi nell’intervallo determinato da quelli inseriti nello step 1 e ne verrà calcolata la media di questi n valori mediante l’algoritmo di Knuth. Per rendere il corpo del programma meno complesso possibile ho sfruttato cicli iterativi For e For Each: più compatti del Do While. Infine questo programma è stato modificato in modo tale da funzionare allo stesso modo anche inserendo una coppia di numeri dispari. Differenza fondamentale che possiamo osservare in questo programma rispetto a quello corrispondente in VB.Net è la maggiore attenzione prestata ai calcoli aritmetici. Il linguaggio C#, infatti, è molto più fiscale sui Tipi dei Dati rispetto a VB.Net e per questo, quando viene calcolata la media (espressa come una variabile Double), bisogna assicurarsi che l’operazione che determina il suo ciclico aggiornamento sia compatibile con questa dichiarazione. Perciò è stata resa necessaria una conversione dei tipi delle variabili relative al calcolo della media.
• ListaC: questo programma permette di creare una lista di numeri interi che si trovano tra un valore minimo ed un valore massimo scelti dall’utilizzatore. Inoltre restituirà in output la lista appena creata, la media di questi n valori, la media degli (n-1) valori più piccoli e la varianza totale. Le due media sono calcolate mediante l’algoritmo di Knuth mentre il calcolo della varianza sfrutta l’algoritmo di Welford
• BinomialC: questo programma restituisce il fattoriale più elevato possibile per i tre tipi presi in considerazione (int, long e Biginteger). Inoltre verrà utilizzata la struttura Try Catch per gestire le eccezioni di Overflow che si verificano incrementando il numero di cui vogliamo calcolare il fattoriale: una volta superato il limite superiore concesso dal tipo che stiamo studiando la struttura Try Catch bloccherà il programma e questo ci permetterà di vedere in output il numero intero il cui fattoriale si avvicina il più possibile al limite del tipo senza superarlo. Questo è un modo più pratico per vedere come a tipi diversi possano corrispondere intervalli di rappresentabilità diversi.
• CovarianzaC: in questo programma si fa riferimento ai due algoritmi utilizzati in precedenza per calcolare la media e la varianza di una lista di valori senza incorrere in errori computazionali e si aggiunge un’ulteriore funzione che, ricevendo in input due liste di valori di uguale lunghezza, permette di calcolarne la covarianza
• FattorialeC: questo programma offre due metodi distinti per calcolare il fattoriale di un numero intero: il metodo standard (o Naive) e quello che si basa sull’algoritmo Binary Split. Verrà inoltre utilizzata la funzione StopWatch che permette di cronometrare il tempo necessario a questi due metodi per calcolare lo stesso fattoriale: in tal modo possiamo provare che l’algoritmo Binay Split risulta più efficiente.
• Regressione_C: questo programma prende in esame in dataset di 200 pazienti affetti da problemi cardiaci e per ciascuno dei quali verrà presa in considerazione l’età e la frequenza cardiaca massima al fine di determinare una retta di regressione. Verrà inoltre restituito in output il coefficiente di accostamento R^2 (che mostra in che proporzione la varianza della retta di regressione spiega la varianza totale) pari a 0.03
• RegressioneListaC: questo programma è in grado di leggere file di testo in 2 modi: trascinando il file o utilizzando una finestra di dialogo. Dopo aver selezionato il file contenente due variabile e infinite unità, sarà possibile creare un modello di regressione lineare. 
• DistrBivariate_C: in questo programma è stato applicato l’inserimento del calcolo delle distribuzioni semplici e bivariate delle variabili di interesse della precedente applicazione.

I seguenti programmi sono stati scritti usando solamente il linguaggio VB

• RettangoloMagico: in questo programma abbiamo esteso la funzionalità della classe di chart interattivo (in VB.NET o C#) aggiungendo la capacità di ridimensionare il rettangolo ponendo il mouse sui lati o sugli angoli del rettangolo e altre eventuali funzionalità che pensate possano essere utili (es. rotazioni, etc.).
• StochProcess_Es1: indicando i valori richiesti dalle caselle visibili, sono state generate delle sample path (di numero pari al numero di iterazioni effettuate). Nella prima finestra si ha una rappresentazione ASCII della distribuzione di frequenza al tempo finale, nella seconda finestra si ha una rappresentazione grafica di tutte le path e nella terza finestra si ha un istogramma per le distribuzioni di frequenza dei prezzi al tempo finale.
• StochProcess2: Nella seconda applicazione si ha un formato analogo alla precedente, dove in più va indicato il tempo intermedio per cui si vuole calcolare la distribuzione di frequenza e non è più presente il tick. Nelle finestre sono presenti le stesse rappresentazioni dell’esecizio 1, ma nella terza finstra si ha l’istogramma delle frequenze sia per i prezzi al tempo finale sia per i prezzi al tempo intermedio.

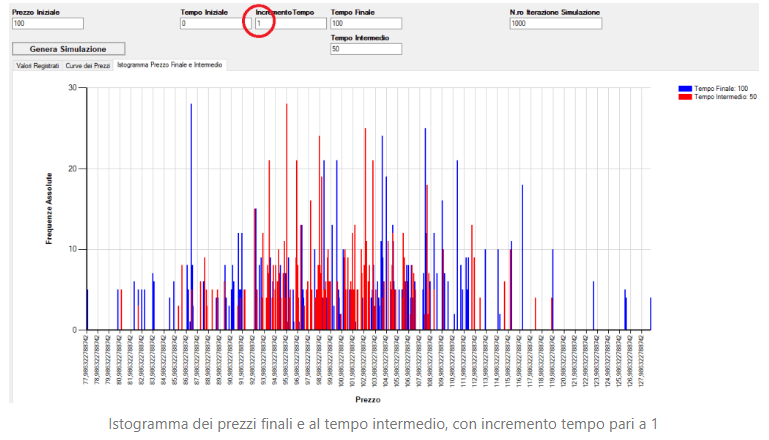
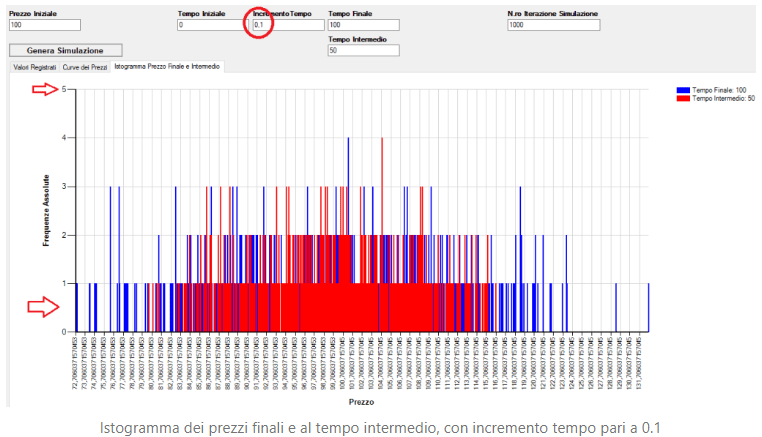
Notiamo come per Δt → 0 (si nota dalle distribuzioni di frequenza sottostanti) le frequenze assolute tendono a diminuire sempre più per i valori vicino a prezzo iniziale, tanto da avere molti valori dei prezzi, sia per il tempo finale che per il tempo intermedio, con frequenza assoluta pari a 1. Questo indica che un incremento di tempo sempre minore per questo tipo di variazione dei prezzi porta ad avere una maggiore incertezza sul valore esatto del prezzo ad un determinato tempo.

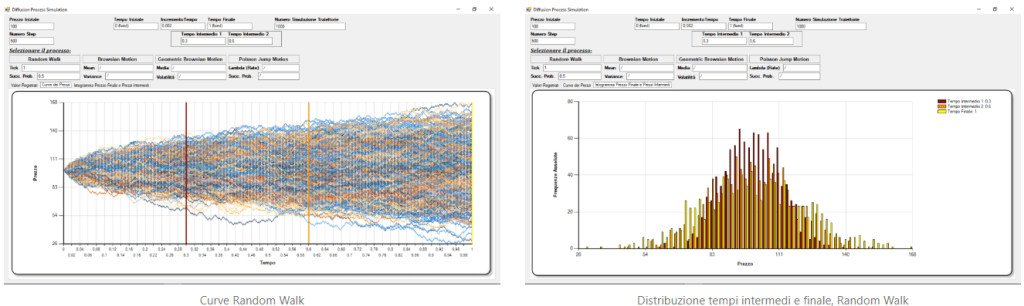
• Es2Modificato: questo programma è il miglioramento a livello grafico dell’esercizio precedente, il quale è stato anche completato mediante l’aggiunta del Geometric Brownian Motion e del Processo di Poisson.
• Esercizio 19-20:
  • Punto A) Raccogliere (da Internet) e testare (con grafico/simulazione) programmi/snippets per: 1)i principali generatori di numeri pseudocasuali; 2)Distribuzioni discrete qualsiasi: Inversione della CDF, “Alias” method; 3)Principali discrete: Bernoulli, Binomiale, Ipergeometrica, Poisson, etc. 4)Principali continue: Normale, Esponenziale, Weibull, Lognormale, Gamma, (Chi quadro, F Fisher, T Student),  etc.
  • Punto B)  Raccogliere (su Internet) e testare programmi/snippets per il calcolo delle probabilità per le principali distribuzioni discrete: Binomiale, Ipergeometrica, Poisson

'NORMALE 
Private Function Normale(ByVal mean As Double, ByVal stdDev As Double) As Double
'metodo di Marseglia
 
Static spare As Double
Static hasSpare As Boolean = False
If hasSpare Then
hasSpare = False
Return spare * stdDev + mean
Else
Dim u, v, s As Double
Do
u = rand.NextDouble * 2.0 - 1.0
v = rand.NextDouble * 2.0 - 1.0
s = u * u + v * v
Loop While s >= 1.0 OrElse s = 0.0
s = Math.Sqrt(-1.0 * Math.Log(s) / s)
spare = v * s
hasSpare = True
Return mean + stdDev * u * s
End If
End Function
 
 
'LOGNORMALE
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function LogNormale(mean As Double, stdDev As Double) As Double
Return (Math.Exp(Me.Normale(mean, stdDev)))
End Function
 
'ESPONENZIALE      
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Esponenziale(beta As Double) As Double
Dim U As Double = rand.NextDouble
Dim out As Double = -beta * Math.Log(U)
Return out
End Function
 
'CHI-QUADRO        
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function ChiSquare(df As Integer) As Double
Dim somma As Double = 0
df = CInt(df / 2)
For d = 1 To df
somma += Math.Log(rand.NextDouble)
Next
Return (-2 * somma)
End Function
 
 
'WEIBULL           
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Weibull(gamma As Double, beta As Double) As Double
Return (Math.Pow(Me.Esponenziale(beta), 1 / gamma))
End Function
 
 
'T DI STUDENT      
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function tStudent(df As Integer) As Double
Return (Me.Normale(0, 1) / Math.Sqrt(Me.ChiSquare(df) / df))
End Function
 
 
'GAMMA             
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Gamma(a As Double, b As Double) As Double
Dim somma As Double = 0
For h As Double = 1 To a
somma += Math.Log(rand.Next)
Next
Return -b * somma
End Function
 
 
'F-FISHER           
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function FFisher(df1 As Integer, df2 As Integer) As Double
Dim Num As Double = Me.ChiSquare(df1) / df1
Dim Den As Double = Me.ChiSquare(df2) / df2
Return (Num / Den)
End Function
 
 
'BERNOULLI
Private Function Bernoulli(p As Double) As Integer
Dim Risultato As Integer
Risultato = If(rand.NextDouble > p, 1, 0)
Return Risultato
End Function
 
 
'IPERGEOMETRICA       
'https://peteroupc.github.io/randomfunc.html#Hypergeometric_Distribution
Private Function Ipergeometrica(trials As Integer, ones As Integer, count As Integer) As Integer
If ones < 0 OrElse count < 0 OrElse trials < 0 OrElse ones > count OrElse trials > count Then Me.RichTextBox1.Text = "Errore"
If ones = 0 Then Return 0
Dim i As Integer = 0
Dim successi As Integer = 0
Dim CountCorrente As Integer = count
Dim OnesCorrente As Integer = ones
While i < trials AndAlso OnesCorrente > 0
If Me.Bernoulli(OnesCorrente / CountCorrente) = 1 Then
OnesCorrente -= 1
successi += 1
End If
CountCorrente -= 1
i += 1
End While
Return successi
End Function
 
'BINOMIALE    
'https://cs.stackexchange.com/questions/48669/how-to-improve-the-binomial-algorithm
Private Function Binomiale(n As Integer, k As Integer, p As Double) As Double
If (n = 0 AndAlso k = 0) Then Return 1
If (n < 0 OrElse k < 0) Then Return 0
Return (1 - p) * Binomiale(n - 1, k, p) + p * Binomiale(n - 1, k - 1, p)
End Function
 
'POISSON       
'http://www.nrbook.com/devroye/Devroye_files/chapter_ten.pdf
Private Function Poisson(beta As Double, lambda As Double) As Double
Dim X As Double = 0
Dim Somma As Double = 0
While True
Do
Dim variabile As Double = Me.Esponenziale(beta)
Somma += variabile
If Somma < lambda Then
X += 1
Else
Return (X)
End If
Loop
End While
End Function
 
 
'PROBABILITA' BINOMIALE
Private Function ProbabilitaBinomiale(tentativi As Integer, p As Double)
Dim cont As Integer = 0
For h As Integer = 1 To tentativi
If rand.NextDouble > p Then
cont += 1
End If
Next
Return CDbl(cont / tentativi)
End Function
 
 
'PROBABILITA' POISSON         
'metodo di MonteCarlo
Private Function ProbabilitaPoisson(x As Integer, ripetizioni As Integer, beta As Double, lambda As Double) As Double
Dim contatore As Integer = 0
For h As Integer = 1 To ripetizioni
If CInt(Me.Poisson(beta, lambda)) = x Then contatore += 1
Next
Return (CDbl(contatore / ripetizioni))
End Function
 
 
'PROBABILITA' IPERGEOMETRICA   
'metodo di MonteCarlo
Private Function ProbabilitaIpergeometrica(x As Integer, ripetizioni As Integer, trials As Integer, ones As Integer, count As Integer) As Double
Dim contatore As Integer = 0
For h As Integer = 1 To ripetizioni
If CInt(Me.Ipergeometrica(trials, ones, count)) = x Then contatore += 1
Next
Return (CDbl(contatore / ripetizioni))
End Function

• Es2Modificato: questo programma è il miglioramento a livello grafico dell’esercizio precedente, il quale è stato anche completato mediante l’aggiunta del Geometric Brownian Motion e del Processo di Poisson.

Esercizio 19-20:

• Punto A) Raccogliere (da Internet) e testare (con grafico/simulazione) programmi/snippets per: 1)i principali generatori di numeri pseudocasuali; 2)Distribuzioni discrete qualsiasi: Inversione della CDF, “Alias” method; 3)Principali discrete: Bernoulli, Binomiale, Ipergeometrica, Poisson, etc. 4)Principali continue: Normale, Esponenziale, Weibull, Lognormale, Gamma, (Chi quadro, F Fisher, T Student),  etc.
• Punto B)  Raccogliere (su Internet) e testare programmi/snippets per il calcolo delle probabilità per le principali distribuzioni discrete: Binomiale, Ipergeometrica, Poisson

'NORMALE 
Private Function Normale(ByVal mean As Double, ByVal stdDev As Double) As Double
'metodo di Marseglia
 
Static spare As Double
Static hasSpare As Boolean = False
If hasSpare Then
hasSpare = False
Return spare * stdDev + mean
Else
Dim u, v, s As Double
Do
u = rand.NextDouble * 2.0 - 1.0
v = rand.NextDouble * 2.0 - 1.0
s = u * u + v * v
Loop While s >= 1.0 OrElse s = 0.0
s = Math.Sqrt(-1.0 * Math.Log(s) / s)
spare = v * s
hasSpare = True
Return mean + stdDev * u * s
End If
End Function
 
 
'LOGNORMALE
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function LogNormale(mean As Double, stdDev As Double) As Double
Return (Math.Exp(Me.Normale(mean, stdDev)))
End Function
 
'ESPONENZIALE      
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Esponenziale(beta As Double) As Double
Dim U As Double = rand.NextDouble
Dim out As Double = -beta * Math.Log(U)
Return out
End Function
 
'CHI-QUADRO        
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function ChiSquare(df As Integer) As Double
Dim somma As Double = 0
df = CInt(df / 2)
For d = 1 To df
somma += Math.Log(rand.NextDouble)
Next
Return (-2 * somma)
End Function
 
 
'WEIBULL           
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Weibull(gamma As Double, beta As Double) As Double
Return (Math.Pow(Me.Esponenziale(beta), 1 / gamma))
End Function
 
 
'T DI STUDENT      
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function tStudent(df As Integer) As Double
Return (Me.Normale(0, 1) / Math.Sqrt(Me.ChiSquare(df) / df))
End Function
 
 
'GAMMA             
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function Gamma(a As Double, b As Double) As Double
Dim somma As Double = 0
For h As Double = 1 To a
somma += Math.Log(rand.Next)
Next
Return -b * somma
End Function
 
 
'F-FISHER           
'https://www.encyclopediaofmath.org/index.php/Generating_random_variables
Private Function FFisher(df1 As Integer, df2 As Integer) As Double
Dim Num As Double = Me.ChiSquare(df1) / df1
Dim Den As Double = Me.ChiSquare(df2) / df2
Return (Num / Den)
End Function
 
 
'BERNOULLI
Private Function Bernoulli(p As Double) As Integer
Dim Risultato As Integer
Risultato = If(rand.NextDouble > p, 1, 0)
Return Risultato
End Function
 
 
'IPERGEOMETRICA       
'https://peteroupc.github.io/randomfunc.html#Hypergeometric_Distribution
Private Function Ipergeometrica(trials As Integer, ones As Integer, count As Integer) As Integer
If ones < 0 OrElse count < 0 OrElse trials < 0 OrElse ones > count OrElse trials > count Then Me.RichTextBox1.Text = "Errore"
If ones = 0 Then Return 0
Dim i As Integer = 0
Dim successi As Integer = 0
Dim CountCorrente As Integer = count
Dim OnesCorrente As Integer = ones
While i < trials AndAlso OnesCorrente > 0
If Me.Bernoulli(OnesCorrente / CountCorrente) = 1 Then
OnesCorrente -= 1
successi += 1
End If
CountCorrente -= 1
i += 1
End While
Return successi
End Function
 
'BINOMIALE    
'https://cs.stackexchange.com/questions/48669/how-to-improve-the-binomial-algorithm
Private Function Binomiale(n As Integer, k As Integer, p As Double) As Double
If (n = 0 AndAlso k = 0) Then Return 1
If (n < 0 OrElse k < 0) Then Return 0
Return (1 - p) * Binomiale(n - 1, k, p) + p * Binomiale(n - 1, k - 1, p)
End Function
 
'POISSON       
'http://www.nrbook.com/devroye/Devroye_files/chapter_ten.pdf
Private Function Poisson(beta As Double, lambda As Double) As Double
Dim X As Double = 0
Dim Somma As Double = 0
While True
Do
Dim variabile As Double = Me.Esponenziale(beta)
Somma += variabile
If Somma < lambda Then
X += 1
Else
Return (X)
End If
Loop
End While
End Function
 
 
'PROBABILITA' BINOMIALE
Private Function ProbabilitaBinomiale(tentativi As Integer, p As Double)
Dim cont As Integer = 0
For h As Integer = 1 To tentativi
If rand.NextDouble > p Then
cont += 1
End If
Next
Return CDbl(cont / tentativi)
End Function
 
 
'PROBABILITA' POISSON         
'metodo di MonteCarlo
Private Function ProbabilitaPoisson(x As Integer, ripetizioni As Integer, beta As Double, lambda As Double) As Double
Dim contatore As Integer = 0
For h As Integer = 1 To ripetizioni
If CInt(Me.Poisson(beta, lambda)) = x Then contatore += 1
Next
Return (CDbl(contatore / ripetizioni))
End Function
 
 
'PROBABILITA' IPERGEOMETRICA   
'metodo di MonteCarlo
Private Function ProbabilitaIpergeometrica(x As Integer, ripetizioni As Integer, trials As Integer, ones As Integer, count As Integer) As Double
Dim contatore As Integer = 0
For h As Integer = 1 To ripetizioni
If CInt(Me.Ipergeometrica(trials, ones, count)) = x Then contatore += 1
Next
Return (CDbl(contatore / ripetizioni))
End Function

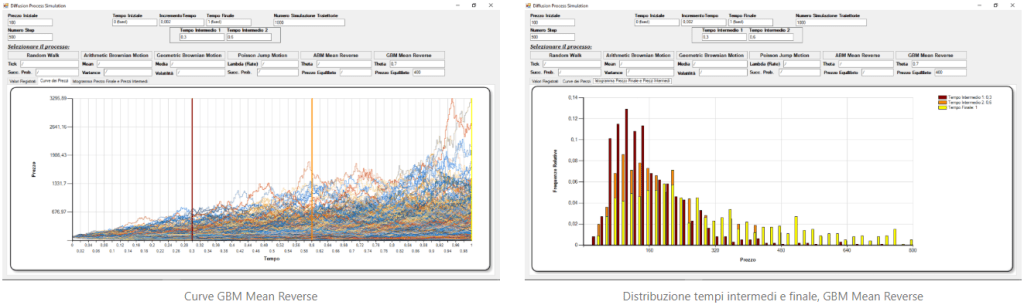
• Es2Completo: nel seguente programma si ha un ulteriore miglioramento dell’ Esercizio 2, con l’aggiunta di due modelli con Mean Reversio, uno per incrementi aritmetico, uno per incrementi geometrici. Nella specificazione dei due metodi è importante specificare il valore Theta (fissato in entrambi i casi a 0.7) che rappresenta un indice di quanto la curva di prezzi si riesce ad avvicinare al Prezzo d’equilibrio stabilito.Il prezzo di equilibrio per la GBM Mean Reverse è fissato pari a 500, mentre per l’ABM Mean Reverse è fissato pari a 5, in quanto il prezzo iniziale deve essere pari a 0.

• CalcoloPNL_Componenti: Nell’applicazione caricata si ha una rappresentazione grafica del lot matching con anche il calcolo PNL e una rappresentazione grafica del PNL. Premendo il tasto Start dell’applicazione, si avvia una simulazione di ordini Sell/Buy che avviene ogni secondo in maniera pseudo-casuale e viene contemporaneamente calcolato il PNL con annessa rappresentazione grafica.Premendo il tasto Stop si interrompe la simulazione in esecuzione e premendo nuovamente il tasto Start di avvia una nuova simulazione.

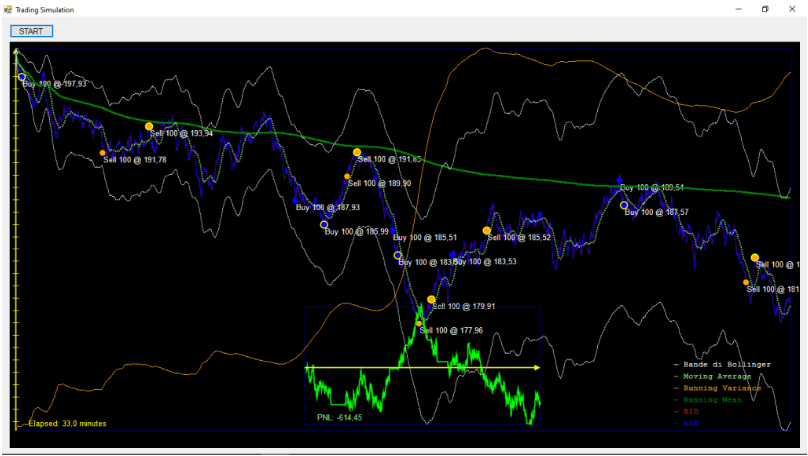
• TradingSimulation: L’esercizio 4 presenta la seguente struttura: processo aleatorio + ordini e calcolo PNL. Viene poi completato aggiungendo i 4 indicatori quantitativi Running Mean, Moving Averages, Moving STD, Bollinger Bands.Nell’applicazione caricata si ha una rappresentazione di una curvadei prezzi (BID e ASK) con la generazione di ordini Sell o Buy. Si ha quindi il calcolo del PNL e una rappresentazione grafica.Si hanno inoltre i 4 indicatori quantitativi richiesti: Running Mean, Moving Averages, Moving STD, Bollinger Bands.