I coefficienti binomiali ricoprono un ruolo particolarmente importante all’interno della Sorted List. Tuttavia, prima di entrare nel dettaglio conviene iniziare dalle basi. Consideriamo i numeri da 1 a n e calcoliamo le possibili permutazioni (ossia in quanti modi questi numeri si possono disporre). Non è difficile arrivare alla conclusione che la risposta a questa domanda sia pari ad n! (n fattoriale), il quale è pari al prodotto di tutti gli interi tra 1 ed n:
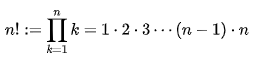
Una volta chiarito il concetto di permutazione si può estendere quest’ultimo al caso in cui è espressa anche la numerosità insita in ogni permutazione. Supponiamo infatti di avere i soliti n numeri e di voler calcolare il numero di possibili permutazioni di numerosità k (con k minore o uguale di n): esso sarà pari a
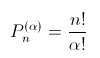
Ora che abbiamo definito le permutazioni possiamo passare alle combinazioni. Qual è la differenza tra le due? Le combinazioni non danno peso all’ordine degli elementi al loro interno (ad esempio, la combinazione 1,2,3 risulta identica alla combinazione 3,2,1). Ciò significa che a parità di numerosità degli elementi una combinazione di classe k equivale a k! permutazioni e pertanto
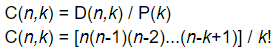
Elenchiamo adesso le proprietà dei coefficienti binomiali, che ci saranno utili per fini computazionali:
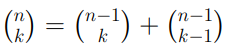
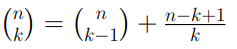
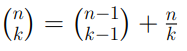
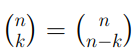
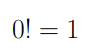
Le ultime due proprietà prendono rispettivamente il nome di Proprietà di simmetria e dello zero fattoriale.