Relazioni di ricorrenza per la covarianza

Le relazioni di ricorrenza sono utili per costruire algoritmi numericamente stabili. Finora abbiamo analizzato relazioni di ricorrenza inerenti al calcolo della media e della varianza facendo riferimento rispettivamente all’algoritmo di Knuth e di Welford. Tuttavia esiste una relazione di questo tipo anche per la covarianza ma prima di introdurla è necessario partire dalla definizione classica di questo indice.

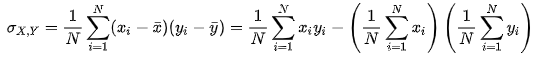
La covarianza può essere calcolata solo all’interno di un contesto bivariato e cioè in cui rilevo due variabili distinte (che indicheremo con X e Y) per ogni unità presa in esame. Supponiamo, ad esempio, di voler calcolare la covarianza tra il peso e la statura di una classe composta da N studenti. Immaginiamo adesso di prendere in esame solo uno di loro e di conoscere il peso e la statura media della classe: se questo studente avesse un peso ed una statura maggiore della media la covarianza assumerebbe un valore positivo (si otterrebbe lo stesso esito anche prendendo in esame uno studente con peso ed una statura minore della media della classe). Questi sono due esempi di associazione diretta. Ovviamente, nel caso in cui la covarianza assumesse valore negativo ci troveremmo davanti ad un’associazione inversa. E’ possibile costruire un indice ottenuto come normalizzazione della covarianza: il coefficiente di correlazione di Pearson.

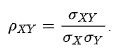
Questo indice è calcolato come il rapporto tra la covarianza tra le due variabili e il suo valore massimo, pari al prodotto delle varianze di X e Y, entrambe sotto radice. Si può dimostrare che il denominatore è pari al valore massimo della covarianza mediante la disuguaglianza di Chauchy-Schwarz

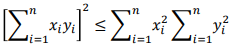
Dal momento che questa disuguaglianza ha validità generale, possiamo renderla più
significativa per i nostri fini applicandola a variabili scarto. In questo modo è possibile riformulare la disuguaglianza nei termini seguenti:

Il risultato appena ottenuto può essere ulteriormente modificato in modo tale da ricondurci agli indici che ci interessano:

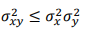
In sintesi, date due variabili statistiche 𝑿 e 𝒀, tramite la disuguaglianza di Cauchy-Schwarz abbiamo dimostrato che la covarianza al quadrato è inferiore o al limite uguale al prodotto tra le rispettive varianze, con il segno di uguaglianza che vale solo nel caso in cui 𝑿 e 𝒀 sono proporzionali tra loro, cioè quando tra queste variabili sussiste un legame lineare.