Date due variabili X e Y risulta interessante determinare l’esistenza di una relazione matematica tra di loro. Una delle relazioni più semplici è la regressione lineare, che ci permette rappresentare la relazione tra X e Y mediante una retta. Dato un generico data set (x_i,y_i) per i=1,…,n il nostro obiettivo sarà quello di determinare l’equazione di una ratta che rappresenta il più possibile la relazione tra X e Y. Per raggiungere il nostro scopo iniziamo prendendo in considerazione un generico punto del data set di coordinate (x_i, y_i) e introduciamo y*_i, cioè il valore che y_i assumerebbe se si trovasse sulla nostra retta. Consideriamo adesso la distanza, in valore assoluto, tra y_i e y*_i: uno dei criteri da utilizzare per determinare l’equazione della retta è quello ci minimizzare la somma delle distanze tra y_i e y*_i per ogni unità del data set: infatti la retta che cerchiamo è quella per cui la somma di queste distanze assume valore minimo. Per minimizzare la somma delle distanze (che da ora in poi indicheremo con S) consideriamo la generica equazione di una retta

Questo ci permetterà di modificare la forma di S come segue

Adesso dobbiamo calcolare la derivata di S rispetto ai due coefficienti alpha e beta e le dovremo porre pari a zero
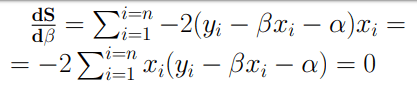

Adesso, ponendo queste due equazioni a sistema, riusciremo facilmente a trovare le equazioni di alpha e beta

Questo sistema ci porta alla conclusione che
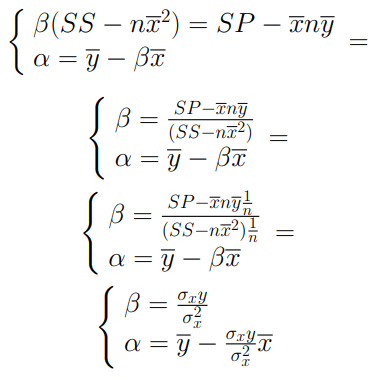
Pertanto la retta che meglio descrive la relazione tra X ed Y sarà la seguente
