Come già sappiamo, la varianza di un data set di unità ci permette di capire quanto questi ultimi si discostano dalla loro media. Tuttavia, nello studio della regressione lineare è possibile scomporre la varianza in modo tale da tener conto non soltanto dei valori y_i ma anche dei corrispettivi y*_i. Cominciamo dalla formula generica della varianza
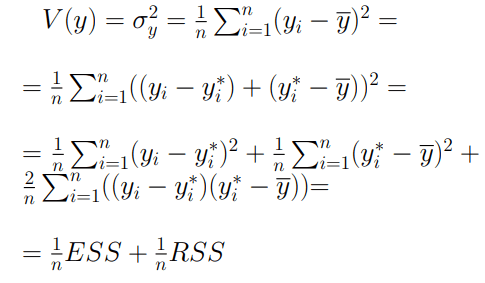
dove ESS rappresenta il numeratore della varianza degli errori (quanto i valori y_i si discostano da y*_i) mentre RSS rappresenta il numeratore della varianza di regressione (la parte della varianza totale spiegata dalla retta di regressione). Se osserviamo con maggiore attenzione la scomposizione della varianza possiamo notare come il doppio prodotto presente nel penultimo passaggio sia stato eliminato: ciò si dimostra come segue. Per prima cosa ricordiamo le relazioni che ci hanno permesso di determinare l’equazione della retta di regressione
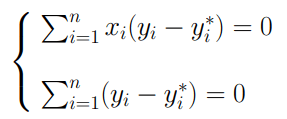
Tenendo a mente che l’equazione della retta di regressione è
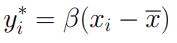
Il doppio prodotto risulterà essere pari a
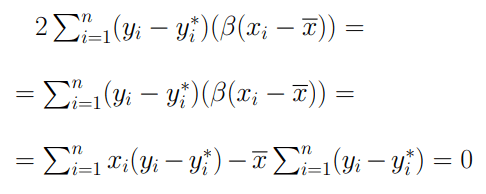
In conclusione, maggiore sarà il rapporto tra RSS e TSS (la varianza totale) migliore sarà la retta di regressione. Questo rapporto prende il nome di Indice di accostamento e si indica con il simbolo R^2