La formula di Legendre e la sua utilità nelle applicazioni

Nel precedente articolo abbiamo descritto alcuni metodi basati sugli operatori bitwise che permettono di sfruttare le relazioni tra valori numerici sotto forma di sequenze di bit. In particolare avevamo descritto come si poteva determinare la massima potenza di un generico n. Quello che affronteremo in questo articolo è la risoluzione di un problema molto simile a quello appena ricordato ma che necessita di un procedimento leggermente diverso: determinare la massima potenza che divide il fattoriale di n. In particolare verrà descritta la risoluzione di questo problema assumendo che la base di questa potenza sia 2 ma non temete, alla fine di questo articolo verranno introdotte le versioni generalizzate di questo procedimento. Utilizzeremo nella risoluzione di questo problema la formula di Legendre secondo cui posso scomporre un qualunque numero M per una qualunque potenza per un altro numero:

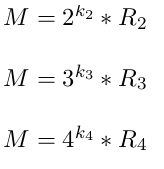
L’esponente è detto valutazione p-adica di M dove p è il numero che sta alla base dell’esponente:

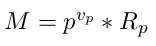
Facciamo un esempio: consideriamo un numero n pari a 17. Il suo fattoriale si ottiene come prodotto dei numeri interi minori o uguali di sé.

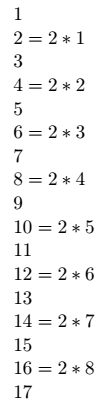
Adesso contiamo i due presenti sulla colonna di destra: sono pari ad 8 (la parte intera di 17/2). Se eliminassimo i 2 appena considerati potremmo ripetere questo procedimento peri termini da 1 a 8.

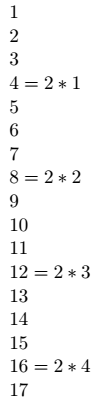
Questa volta il numero di volte in cui compare il 2 è pari a 4 (e cioè alla parte intera di 17/4). Eseguendo iterativamente questo processo otterremo che il numero totale di volte in cui è comparso il 2 sarà pari a 15. Perciò concludiamo dicendo che

dove R equivale a tutti i numeri dispari che non ho considerato nei vari passaggi.

In termini generali, riprendendo la formula in Figura 2, possiamo affermare che v risulta essere pari a

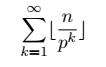
Nel caso in cui n fosse una potenza di 2 (ad esempio 16) potremmo facilmente considerarla come una somma di altre potenze con la stessa base. In questo caso, eseguendo gli stessi calcoli di prima, otterremo che v risulta essere pari a 15 e cioè al valore di n a cui è stato sottratto il numero di bit pari ad 1 che contiene al suo interno. In conclusione, se non volessimo sfruttare la rappresentazione dualica ma ci volessimo limitare al caso generico potremmo dire che la potenza v risulta essere pari a