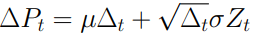Definiamo con processo di Wiener (o Browian Motion) un processo stocastico delimitato su un’asse temporale continua e che presenta le seguenti proprietà:
- W(0)=0 il nostro processo deve avere un punto d’origine (non necessariamente 0). Questo è necessario perché il processo è definito in base agli incrementi
- Continuo in t con probabilità 1
- Presenta incrementi stazionari indipendentemente distribuiti secondo una normale con media 0 e varianza t
Supponiamo di avere una random walk che ha incrementi pari a + o – 1 rispettivamente con probabilità pari a 1/2 (il singolo salto ha questa distribuzione discreta) e consideriamo due istanti t e t+ Δt:
l’incremento non è altro che la somma dei salti avvenuti in questo intervallo di tempo. Vista la distribuzione possiamo dire che la media del salto è 0 mentre la varianza è 1
Quindi anche l’incremento avrà valore atteso pari a 0 mentre la sua varianza sarà pari a Δt (perché i salti sono indipendenti). La varianza è quindi proporzionale alla distanza Δt.
Voglio portare queste conclusione anche nel caso continuo (nella Browian Motion) e quindi assumo che qualunque intervallo prendo la media e la varianza dell’incremento assuma proprio quel valore.
Inoltre assumo che l’incremento sia normale perché essendo una somma di variabili posso immaginare che nel continuo valga il teorema del limite centrale e quindi potrò sostituire la somma di variabili indipendenti ed identicamente distribuite con una normale. Una Brownian Motion presenta anche una forma generalizzata che equivale a considerare un processo con media μ*Δt e varianza pari a σ^2 * Δt. Per quanto riguarda la definizione differenziale del processo di Wiener consideriamo con ΔPt il suo incremento infinitesimo (e cioè l’incremento che si osserva quando Δt tende a 0). Esso sarà pari a
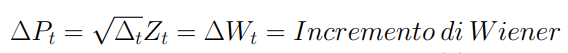
Possiamo affermare inoltre che nel caso generico il valore dell’incremento infinitesimo risulterà pari a