Per capire cosa si intende per moto browniano geometrico mettiamolo a confronto con quello normale (detto anche aritmetico). Esaminiamo il moto browniano aritmetico

Esso presenta la seguente equazione differenziale
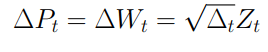
e la seguente generalizzazione
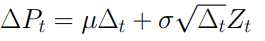
Il moto browniano aritmetico presenta alcuni problemi
- Visto che procedo per incrementi additivi è chiaro che anche se parto da un prezzo iniziale alto, se gli dò molto tempo potrei anche avere valori di prezzo negativi: non è quindi adeguato per studiare i prezzi
- Quando rapportiamo i prezzi di beni o stock non ragioniamo in termini additivi ma in termini di tasso di incremento (return) perché l’importanza di quel bene dipende anche dal prezzo iniziale (l’incremento relativo e non quello assoluto) quindi piuttosto che un modello additivo vorrei quello moltiplicativo e per questo usiamo una brownian motion. geometrica. Il modello moltiplicativo si indica con la seguente formula
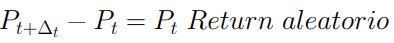
con la seguente equazione differenziale
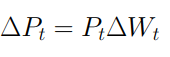
descritta a sua volta in modo più generico mediante la seguente equazione

Nel moto browniano geometrico il differenziale del prezzo non è più la somma di variabili distribuite secondo una normale ma sarà descritta in questo modo e perciò occorre sbarazzarsi del prodotto: per farlo uso la funzione logaritmica
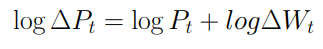
Pertanto la distribuzione di Pt risulta essere di tipo lognormale