I processi di Poisson vengono utilizzati per modellizzare una situazione che presenta salti aleatori. Si tratta di un processo continuous time ma lo spazio degli stati che può assumere è di tipo discreto.
Per definire il processo di Poisson segue le seguenti proprietà:
- Nella sua origini (in genere viene scelto l’istante 0) vale 0
- In ogni intervallo di tempo si può verificare un salto con una certa probabilità
- Nel processo di Poisson si assume ch la probabilità di avere un salto sia pari a λ volte la lunghezza dell’intervallo: più è largo l’intervallo e maggiore sarà la probabilità che avvenga un salto. Il valore di λ deve essere positivo ed esprime il tasso di arrivo di questi eventi (se fosse 10 in un intervallo che va da 0 a 1 vedrei in media 10 salti).
- la probabilità di avere due o più salti in un intervallo di tempo deve tendere a 0 quando Δt tende a 0
Il processo di Poisson può essere approssimato ad una bernoulliana se si tiene in considerazione che in ogni intervallo di tempo si può eseguire un salto con probabilità λ*Δt. Il processo, quindi è una somma di bernoulliane e quindi sarà una distribuzione binomiale: Tuttavia la distribuzione binomiale tende ad una Poisson per Δt che tende a 0 e mantenendo costante λ. A sua volta la Poisson tende ad una normale. Per quanto riguarda i tempi di arrivo, invece, otteniamo una distribuzione uniforme e gli interarrivi (i tempi tra un arrivo e l’altro) hanno una distribuzione esponenziale con par lambda. La distribuzione di poisson è il limite di una distribuzione binomiale per λ uguale a np e n che tende ad infinito. Per dimostrarlo consideriamo che la probabilità che una variabile aleatoria distribuita secondo una binomiale assuma valore pari a k è

Questa formula può essere modificata come segue
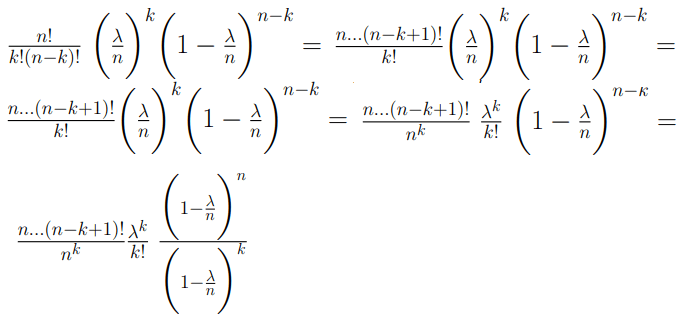
Facendo il limite per n che tende a 

Questa formula equivale alla distribuzione di probabilità di una variabile aleatoria Poisson di parametro λ. Per quanto riguarda i tempi di interarrivi consideriamo la funzione di ripartizione e di densità di una variabile aleatoria esponenziale negativa
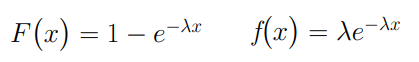
Indichiamo con λ’ il parametro del processo di Poisson che vogliamo valutare. Esso sarà pari a
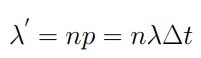
Inoltre, poiché
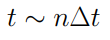
La precedente relazione può essere scritta come

dove λ rappresenta la rate del processo di Poisson. Se adesso prendessimo in considerazione una generica variabile aleatoria Poisson di parametro λ potremmo affermare che
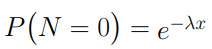
Consideriamo ora un generico range temporale ed identifichiamo con A1 l’intervallo relativo al primo interarrivo. Pertanto avremo che
