Esistono quattro tipi principali di strategie di trading: scalping, day trading, swing trading e position trading. Differenti stili di trading dipendono dal periodo e dalla durata del periodo di apertura.

Scalping Lo scalping è la forma di trading più a breve termine. Questi trader mantengono le posizioni aperte solo per secondi o minuti al massimo. Queste operazioni di breve durata hanno come obiettivo piccoli movimenti dei prezzi infragiornalieri. Lo scopo è quello di fare molte negoziazioni rapide con guadagni più piccoli, ma lasciare che i profitti si accumulino durante il giorno a causa del solo numero di negoziazioni eseguite in ogni sessione di negoziazione.
Day trading I trader giornalieri entrano ed escono dalle loro posizioni nello stesso giorno, eliminando il rischio di grandi spostamenti durante la notte. Alla fine della giornata, chiudono la loro posizione con un profitto o una perdita. Le negoziazioni si svolgono generalmente per un periodo di minuti o ore e, di conseguenza, richiedono tempo sufficiente per analizzare i mercati e monitorare frequentemente le posizioni durante il giorno. Proprio come i commercianti di cuoio capelluto, i commercianti diurni fanno affidamento su piccoli guadagni frequenti per costruire profitti.
Swing trading A differenza dei day trader che detengono posizioni per meno di un giorno, i traders swing in genere mantengono posizioni per diversi giorni, anche se a volte per alcune settimane. Poiché le posizioni vengono mantenute per un certo periodo di tempo, al fine di cogliere movimenti di mercato a breve termine, gli operatori non devono sedersi costantemente monitorando i grafici e le loro operazioni durante il giorno
Position trading I trader di posizione sono focalizzati sul movimento dei prezzi a lungo termine, cercando i massimi profitti potenziali da ottenere da importanti cambiamenti di prezzo. Di conseguenza, le negoziazioni generalmente si estendono per un periodo di settimane, mesi o addirittura anni. I trader di posizione tendono a utilizzare i grafici dei prezzi settimanali e mensili per analizzare e valutare i mercati, utilizzando una combinazione di indicatori tecnici e analisi fondamentali per identificare i potenziali livelli di entrata e uscita
 , contenente i valori osservati di una variabile
, contenente i valori osservati di una variabile  dal tempo 1 al tempo
dal tempo 1 al tempo  , siano:
, siano: il numero dei periodi precedenti a
il numero dei periodi precedenti a  ;
; il numero dei periodi successivi a
il numero dei periodi successivi a  il peso da attribuire all’
il peso da attribuire all’ -esimo valore osservato;
-esimo valore osservato;
 è il periodo o l’ordine della media mobile, ed equivale al numero degli addendi
è il periodo o l’ordine della media mobile, ed equivale al numero degli addendi (in tal caso, si tratta di una normale media aritmetica);
(in tal caso, si tratta di una normale media aritmetica); ;
; per ogni
per ogni  compreso tra 1 e
compreso tra 1 e 
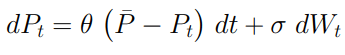
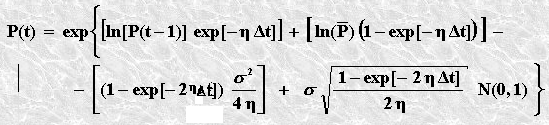

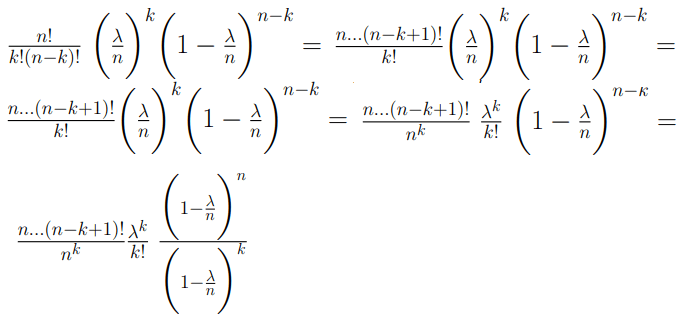
 la formula appena ottenuta si modificherà in questo modo
la formula appena ottenuta si modificherà in questo modo