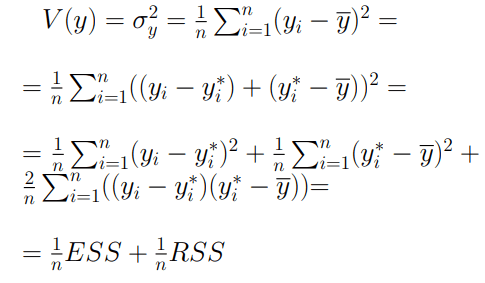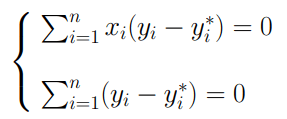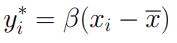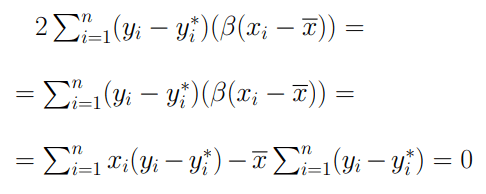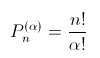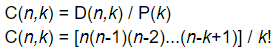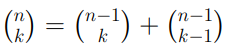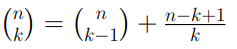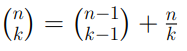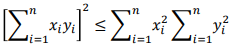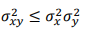Consideriamo un generico valore intero n e la sua traduzione sotto forma di sequenze di bit: quello che vogliamo è determinare il valore assunto dal bit che occupa la prima posizione partendo da destra. In base a quanto detto nell’articolo relativo ai codici binari, il valore che stiamo cercando sarà quello meno significativo e prende perciò il nome di LSB. Per capire come raggiungere il nostro obiettivo consideriamo un generico numero intero n tradotto in sequenza di bit: 1010101. Il metodo più semplice che ci porta alla soluzione cercata consiste nell’utilizzo del comando “and” tra n ed il valore 1: come sappiamo, infatti, questo comando restituisce 1 se i bit che occupano la stessa posizione tra n ed 1 sono uguali, altrimenti restituirà 0. Pertanto avremo il seguente output

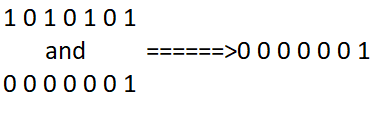
Possiamo concludere affermando che questo metodo applica una maschera ai primi 6 bit lasciando invariato quello che ci interessava.

Il comando “and” che abbiamo appena visto ci ha permesso di individuare il bit meno significativo di un generico valore n. Adesso consideriamo un altro metodo utilizzato nelle operazioni bitwise che consiste nell’azzeramento del primo 1 partendo da destra di un generico valore n. Per comprendere il funzionamento di questo metodo consideriamo la sequenza di numeri interi:

La figura appena introdotta ci permette di notare alcune importanti differenza tra un numero intero n ed il suo precedente (n-1).Qual è la relazione che li lega? Il passaggio da n-1 ad n comporta la sostituzione del primo bit pari a 0 in n-1 con un bit pari a 1 in n. Inoltre, questo incremento renderà pari a 0 tutti i bit che si trovano alla destra di quello appena modificato mentre quelli che si trovano alla sua sinistra rimarranno inalterati. Per comprendere questo ragionamento è sufficiente osservare come varia la sequenza di bit quando si passa, ad esempio, da 3 a 4. Vediamo adesso come questa relazione risulti essere fondamentale per raggiungere il nostro obiettivo. Se eseguissi il comando and tra n e n-1 i valori a sinistra del bit trasformato in 1 a causa dell’incremento rimarrebbero invaiati mentre quelli alla sua destra sarebbero pari a 0: quindi avrei in output un valore uguale ad n con la differenza che al posto dell’1 selezionato avrei 0. Facciamo un esempio tra 3 e 4:

Quello che abbiamo ottenuto, pertanto, è stato ‘azzeramento del primo bit pari ad 1 di n.

Supponiamo, adesso, di voler contare il numero di bit uguali a 1 nella rappresentazione binaria di n. Così come abbiamo fatto per i precedenti operatori bitwise affiancheremo alla spiegazione un esempio, in modo tale da rendere più facile la comprensione del procedimento. Indichiamo, quindi , un valore n sotto forma di sequenza binaria: 10101101. Per contare il numero di bit pari ad 1 contenuto in n esistono diversi metodi. Quello più semplice consiste nell’utilizzare la relazione tra n ed 1 enunciata all’inizio di questo articolo: in questo modo sarà possibile visionare il primo bit di destra di n e, nel caso in cui fosse pari ad 1, verrà contato. Una volta fatto questo utilizziamo degli operatori di shift per traslare verso destra la sequenza di n, eliminando in questo modo il bit precedentemente visionato. Eseguendo iterativamente questo processo riusciremo a contare i bit pari ad 1 contenuti in n. Consideriamo adesso un nuovo algoritmo che restituisce lo stesso output di quello appena descritto ma che risulta essere più rapido di quello naive. Per questo secondo algoritmo ,che prende il nome di Algoritmo di Kernighan, dovremo utilizzare la relazione esistente tra n ed n-1. Notiamo subito come questo algoritmo presenti un numero di passaggi inferiori rispetto a quello naive: si passa, infatti, dal numero di bit al numero di bit pari ad 1. Questo perché in ogni n and n-1 resetto il bit=1 più a destra. quindi questo algoritmo consiste nel loop di n and n-1.

Altra operazione bitwise: nel caso in cui il comando n and n-1 restituisse 0 come soluzione potremmo affermare che n è una potenza di 2.

Consideriamo adesso l’operatore shift. Se eseguissi un comando shift verso destra otterrei che ad ogni 1 del nostro n risulterà associata una potenza inferiore (da 2^k a 2^(k-1)): viene divisa, quindi per 2. Questa divisione per 2 avviene solo se il numero di partenza è pari: in contrario perderemmo il primo bit di destra. Si verifica quindi una divisione troncata: con lo shift prendo la parte intera di n/2. Facciamo un esempio:

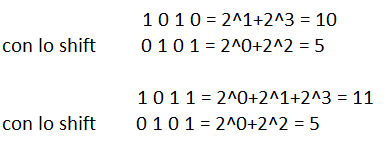
Se avessi eseguito lo shift verso sinistra avrei avuto una situazione opposta. Ovviamente è possibile eseguire di k e non necessariamente di 1: in quel caso avrei ottenuto delle modifiche di 2^k con k positivo o negativo a seconda della direzione dello shift.

Altra operazione: n or 1

Se il numero n è dispari non si modifica mentre se è pari viene incrementato di n: il comando or trasforma n nel primo intero dispari maggiore o uguale di sé.

Altro problema risolto dagli operatori bitwise: partendo da un numero intero n voglio trovare la più grande potenza di 2 lo divide. Detto in modo diverso, voglio essere in grado di esprimere n come 2^k*D dove D è l’intero dispari che residua come fattore. Facciamo un esempio, ponendo n=12 possiamo scomporlo nel prodotto tra 2 e 6, dove 6 più essere a sua volta espresso come prodotto di 2*3. Quindi in questo caso n risulta essere pari a 2^2*3 e pertanto la massima potenza che divide n sarà pari a 2. Ovviamente, se n fosse dispari la potenza massima che stiamo cercando sarebbe pari a 0. Un primo procedimento è stato appena descritto nell’esempio ma ora useremo gli operatori bitwise e la particolare struttura di n-1. Prendiamo in esame un generico numero pari (101000): esso sarà pari a 2^3*(1+2^2) e perciò la sua potenza massima risulta essere pari a 3. Il valore appena ottenuto coincide con la potenza del bit che ha assunto valore pari ad 1 mediante il passaggio da n-1 a n. Eseguendo il comando “not” su n-1 mediante il quale invertiamo gli 1 e gli 0. Questa modifica risulta fondamentale perché eseguendo in comando and tra n e not(n-1) riusciremo a spianare tutti i valori che si trovano alla sinistra del bit modificato a causa dell’incremento in modo tale che rimanga solo l’1 associato alla potenza massima di n.

dove k rappresenta la massima potenza di n.

In questo articolo potrete osservare alcuni esempi di operatori bitwise scritti utilizzando il linguaggio C#

//operatore AND
int a = 74;
int b = 174;
int c = a & b;
this.RichTextBox.Text = "a vale " + a + ", b vale " + b + ", c, ottenuto con l'operatore AND vale " + c + Environment.NewLine;
this.RichTextBox.AppendText("in linguaggio binario si ha " + Convert.ToString(a,2) + " & " + Convert.ToString(b,2) + " = " + Convert.ToString(c,2) + Environment.NewLine + Environment.NewLine);

//operatore OR
int a = 74;
int b = 174;
int c = a | b;
this.RichTextBox.AppendText("a vale " + a + ", b vale " + b + ", c, ottenuto con l'operatore OR vale " + c + Environment.NewLine);
this.RichTextBox.AppendText("in linguaggio binario si ha " + Convert.ToString(a,2) + " | " + Convert.ToString(b,2) + " = " + Convert.ToString(c,2) + Environment.NewLine + Environment.NewLine);

//operatore XOR
int a = 74;
int b = 174;
int c = a ^ b;
this.RichTextBox.AppendText("a vale " + a + ", b vale " + b + ", c, ottenuto con l'operatore XOR vale " + c + Environment.NewLine);
this.RichTextBox.AppendText("in linguaggio binario si ha " + Convert.ToString(a,2) + " ^ " + Convert.ToString(b,2) + " = " + Convert.ToString(c,2) + Environment.NewLine + Environment.NewLine);

//operatore NOT
int a = 74;
int b = ~a;
this.RichTextBox.AppendText("a vale " + a + ", b vale, ottenuto con l'operatore NOT, " + b + Environment.NewLine);
this.RichTextBox.AppendText("in linguaggio binario si ha " + "~" + Convert.ToString(a,2) + " = " + Convert.ToString(b,2) + Environment.NewLine + Environment.NewLine);

//operatore SHIFT a destra
int a =74;
int b = a<<2;
this.RichTextBox.AppendText("a vale " + a + ", b vale, ottenuto con l'operatore SHIFT a sinistra di 2 posizioni, " + b + Environment.NewLine);
this.RichTextBox.AppendText("in linguaggio binario si ha " + Convert.ToString(a,2) + " <<2 = " + Convert.ToString(b,2) + Environment.NewLine + Environment.NewLine);

//operatore SHIFT a sinistra
int a =74;
int b = a>>2;
this.RichTextBox.AppendText("a vale " + a + ", b vale, ottenuto con l'operatore SHIFT a destra di 2 posizioni, " + b + Environment.NewLine);
this.RichTextBox.AppendText("in linguaggio binario si ha " + Convert.ToString(a,2) + " >>2 = " + Convert.ToString(b,2) + Environment.NewLine + Environment.NewLine);

I comandi appena scritti restituiranno i seguenti output

a vale 74, b vale 174, c, ottenuto con l'operatore AND vale 10
in linguaggio binario si ha 01001010 & 10101110 = 00001010

a vale 74, b vale 174, c, ottenuto con l'operatore OR vale 238
in linguaggio binario si ha 01001010 | 10101110 = 11101110

a vale 74, b vale 174, c, ottenuto con l'operatore XOR vale 228
in linguaggio binario si ha 01001010 ^ 10101110 = 11100100

a vale 74, b vale, ottenuto con l'operatore NOT, 181
in linguaggio binario si ha ~01001010 = 10110101

a vale 74, b vale, ottenuto con l'operatore SHIFT a sinistra di due posizioni, 40
in linguaggio binario si ha 01001010<<2 = 00101000

a vale 74, b vale, ottenuto con l'operatore SHIFT a destra di due posizioni, 18
in linguaggio binario si ha 01001010>>2 = 00010010

In informatica e programmazione, un operatore è un simbolo che specifica quale legge applicare a uno o più operandi, per generare un risultato. Possono essere classificati in base al numero di operandi che richiedono oppure in base alla loro funzionalità. Volendo applicare la prima classificazione potremmo dire che gli operatori si dividono in:

• Unary: Not (in C# presenta forme diverse a seconda se stiamo studiando tipi numeri o Bitwise (~) o booleani (!))
• Binary: +, -, *, /, Xor (che coincide con il ^ in C#)
• Ternary: ?

N.B: il simbolo / assume un funzionamento diverso a seconda del linguaggio di programmazione che stiamo utilizzando: in C# infatti non effettua la conversione automatica dei tipi

Per quanto riguarda la funzionalità, distinguiamo gli operatori in:

• Aritmetici: +, -, *, /, % (che in VB corrisponde a mod)
• Logici: and, or, not (che in c# si indicano con &, |, (!, ~))
• Comparazione (o relazionali): = (in C# corrisponde a ==), <, >, >=, <=, < > (in C# corrisponde a !), is, is not
• Concatenazione: & (in VB), + (in C#)
• Condizionali: andalso, orelse (in VB), &&, || (in C#)

Gli operatori condizionali alimentano il cosiddetto short circuiting: quando uso 2 condizioni, la seconda verrà valutata solo se strettamente necessaria. Invece, per quanto riguarda gli operatori logici i 2 operandi verranno valutati in ogni caso.

Come già sappiamo, la varianza di un data set di unità ci permette di capire quanto questi ultimi si discostano dalla loro media. Tuttavia, nello studio della regressione lineare è possibile scomporre la varianza in modo tale da tener conto non soltanto dei valori y_i ma anche dei corrispettivi y*_i. Cominciamo dalla formula generica della varianza

dove ESS rappresenta il numeratore della varianza degli errori (quanto i valori y_i si discostano da y*_i) mentre RSS rappresenta il numeratore della varianza di regressione (la parte della varianza totale spiegata dalla retta di regressione). Se osserviamo con maggiore attenzione la scomposizione della varianza possiamo notare come il doppio prodotto presente nel penultimo passaggio sia stato eliminato: ciò si dimostra come segue. Per prima cosa ricordiamo le relazioni che ci hanno permesso di determinare l’equazione della retta di regressione

Tenendo a mente che l’equazione della retta di regressione è

Il doppio prodotto risulterà essere pari a

In conclusione, maggiore sarà il rapporto tra RSS e TSS (la varianza totale) migliore sarà la retta di regressione. Questo rapporto prende il nome di Indice di accostamento e si indica con il simbolo R^2

Date due variabili X e Y risulta interessante determinare l’esistenza di una relazione matematica tra di loro. Una delle relazioni più semplici è la regressione lineare, che ci permette rappresentare la relazione tra X e Y mediante una retta. Dato un generico data set (x_i,y_i) per i=1,…,n il nostro obiettivo sarà quello di determinare l’equazione di una ratta che rappresenta il più possibile la relazione tra X e Y. Per raggiungere il nostro scopo iniziamo prendendo in considerazione un generico punto del data set di coordinate (x_i, y_i) e introduciamo y*_i, cioè il valore che y_i assumerebbe se si trovasse sulla nostra retta. Consideriamo adesso la distanza, in valore assoluto, tra y_i e y*_i: uno dei criteri da utilizzare per determinare l’equazione della retta è quello ci minimizzare la somma delle distanze tra y_i e y*_i per ogni unità del data set: infatti la retta che cerchiamo è quella per cui la somma di queste distanze assume valore minimo. Per minimizzare la somma delle distanze (che da ora in poi indicheremo con S) consideriamo la generica equazione di una retta

Questo ci permetterà di modificare la forma di S come segue

Adesso dobbiamo calcolare la derivata di S rispetto ai due coefficienti alpha e beta e le dovremo porre pari a zero

Adesso, ponendo queste due equazioni a sistema, riusciremo facilmente a trovare le equazioni di alpha e beta

Questo sistema ci porta alla conclusione che

Pertanto la retta che meglio descrive la relazione tra X ed Y sarà la seguente

In informatica ,l’uso di tipi numerici a precisione arbitraria permette di eseguire calcoli vengono eseguiti su numeri la cui cifre di precisione sono limitate solo dalla disposizione di memoria del sistema host. Ciò contrasta con l’aritmetica più veloce precisione fissa si trova nella maggior aritmetica logica hardware (ALU), che offre tipicamente tra 8 e 64 bit di precisione. Diversi moderni linguaggi di programmazione sono dotati di supporto per bignum, e altri hanno le librerie disponibili per la precisione arbitraria interi e in virgola mobile per la matematica. Invece di memorizzare i valori da un numero fisso di binari bit relativi alla dimensione del registro del processore , queste implementazioni utilizzano tipicamente lunghezza variabile array di cifre. Un esempio di numeri a precisione arbitraria è rappresentato dal tipo Biginteger. Mediante questo tipo di valori è possibile determinare un intero con segno arbitrariamente grande. Il tipo di BigInteger è un tipo non modificabile che rappresenta un Integer arbitrariamente grande il cui valore in teoria non ha limiti superiori o inferiori. I membri del BigInteger tipo sono strettamente paralleli a quelli di altri tipi integrali (i tipi Byte, Int16, Int32, Int64 e SByte). Questo tipo è diverso dagli altri tipi integrali nel Framework.NET , che hanno un intervallo indicato dalle proprietà MinValue e MaxValue.

Come abbiamo visto, il fattoriale di un numero intero n equivale al prodotto di tutti gli interi minori o uguali del numero selezionato. Tuttavia questo calcolo si rivela sempre più complesso da un punto di vista computazionale man mano che il valore di n cresce. Per questo motivo sono stati introdotti alcuni algoritmi che permettono di calcolare il fattoriale di un numero in modo più rapido: uno tra questi è il metodo Binary Split. Il Binary Split appartiene alla tipologia degli algoritmi Divide et Impera: divide il problema in due problemi più piccoli e li esegue separatamente: ciò permette di ottimizzare i tempi di esecuzione. Supponiamo di avere una lista di n valori interi e consecutivi tra loro

1,2,3,4,5,6,7,8,9

Secondo la definizione classica di fattoriale adesso dovremmo moltiplicare questi 9 numeri per determinare il valore di 9! ma, come abbiamo appena detto, esiste un algoritmo che porta alla stessa soluzione in maniera più rapida. Dividiamo, quindi, questi 9 valori in due sottoclassi il più omogenee possibili per quanto riguarda la numerosità (ho volutamente selezionato un caso in cui i termini di partenza siano dispari, in modo tale da farvi vedere che partire con due sottogruppi di lunghezza diversa non causa alcun problema). Ovviamente il processo di divisione può essere iterato su ogni sottogruppo, finché non si arriva a sottogruppi composti da un solo elemento. Una volta terminato il processo di divisione si può eseguire il prodotto

Il Try Catch è una struttura che intercetta e gestisce le eccezioni che provocano un arresto del programma. Per capire il funzionamento di questa struttura risulta fondamentale il concetto di Call Stack: essa rappresenta la pila delle chiamate che partono dalla funzione corrente fino ad arrivare a quella chiamante. Supponiamo che in una chiamata presente nel programma ci sia un’eccezione. Se nella stessa chiamata è presente anche una struttura Try Catch allora sarà quest’ultima ad operare sull’eccezione ma se così non fosse l’eccezione salirà lungo la Call Stack fino ad arrivare ad una chiamata con un Try Catch al suo interno. Cosa succede se la struttura Try Catch è assente dal programma? In quel caso l’eccezione risalirà la Call Stack fino al punto di entrata del programma, rappresentato da una Main nel linguaggio C# e da un gestore di default in VB.Net. In conclusione, è possibile lanciare un’eccezione all’interno di una Try Catch (mediante la parola chiave Throw): ciò può essere necessario nel caso in cui si volessero fare delle operazioni localmente

I coefficienti binomiali ricoprono un ruolo particolarmente importante all’interno della Sorted List. Tuttavia, prima di entrare nel dettaglio conviene iniziare dalle basi. Consideriamo i numeri da 1 a n e calcoliamo le possibili permutazioni (ossia in quanti modi questi numeri si possono disporre). Non è difficile arrivare alla conclusione che la risposta a questa domanda sia pari ad n! (n fattoriale), il quale è pari al prodotto di tutti gli interi tra 1 ed n:

Una volta chiarito il concetto di permutazione si può estendere quest’ultimo al caso in cui è espressa anche la numerosità insita in ogni permutazione. Supponiamo infatti di avere i soliti n numeri e di voler calcolare il numero di possibili permutazioni di numerosità k (con k minore o uguale di n): esso sarà pari a

Ora che abbiamo definito le permutazioni possiamo passare alle combinazioni. Qual è la differenza tra le due? Le combinazioni non danno peso all’ordine degli elementi al loro interno (ad esempio, la combinazione 1,2,3 risulta identica alla combinazione 3,2,1). Ciò significa che a parità di numerosità degli elementi una combinazione di classe k equivale a k! permutazioni e pertanto

Elenchiamo adesso le proprietà dei coefficienti binomiali, che ci saranno utili per fini computazionali:

Le ultime due proprietà prendono rispettivamente il nome di Proprietà di simmetria e dello zero fattoriale.

Le relazioni di ricorrenza sono utili per costruire algoritmi numericamente stabili. Finora abbiamo analizzato relazioni di ricorrenza inerenti al calcolo della media e della varianza facendo riferimento rispettivamente all’algoritmo di Knuth e di Welford. Tuttavia esiste una relazione di questo tipo anche per la covarianza ma prima di introdurla è necessario partire dalla definizione classica di questo indice.

La covarianza può essere calcolata solo all’interno di un contesto bivariato e cioè in cui rilevo due variabili distinte (che indicheremo con X e Y) per ogni unità presa in esame. Supponiamo, ad esempio, di voler calcolare la covarianza tra il peso e la statura di una classe composta da N studenti. Immaginiamo adesso di prendere in esame solo uno di loro e di conoscere il peso e la statura media della classe: se questo studente avesse un peso ed una statura maggiore della media la covarianza assumerebbe un valore positivo (si otterrebbe lo stesso esito anche prendendo in esame uno studente con peso ed una statura minore della media della classe). Questi sono due esempi di associazione diretta. Ovviamente, nel caso in cui la covarianza assumesse valore negativo ci troveremmo davanti ad un’associazione inversa. E’ possibile costruire un indice ottenuto come normalizzazione della covarianza: il coefficiente di correlazione di Pearson.

Questo indice è calcolato come il rapporto tra la covarianza tra le due variabili e il suo valore massimo, pari al prodotto delle varianze di X e Y, entrambe sotto radice. Si può dimostrare che il denominatore è pari al valore massimo della covarianza mediante la disuguaglianza di Chauchy-Schwarz

Dal momento che questa disuguaglianza ha validità generale, possiamo renderla più
significativa per i nostri fini applicandola a variabili scarto. In questo modo è possibile riformulare la disuguaglianza nei termini seguenti:

Il risultato appena ottenuto può essere ulteriormente modificato in modo tale da ricondurci agli indici che ci interessano:

In sintesi, date due variabili statistiche 𝑿 e 𝒀, tramite la disuguaglianza di Cauchy-Schwarz abbiamo dimostrato che la covarianza al quadrato è inferiore o al limite uguale al prodotto tra le rispettive varianze, con il segno di uguaglianza che vale solo nel caso in cui 𝑿 e 𝒀 sono proporzionali tra loro, cioè quando tra queste variabili sussiste un legame lineare.